Estruturas de Dados I
Filas de Prioridade
Igor Machado Coelho
14/10/2020 - rev. 18/06/2025
Filas de Prioridade
Pré-Requisitos
São requisitos para essa aula:
- Introdução/Fundamentos de Programação (em alguma linguagem de programação)
- Interesse em aprender C/C++
- Noções de tipos de dados
- Noções de listas e encadeamento
- Aula de filas
- Aula de árvores
Tipo Abstrato: Fila de Prioridade
Fila de Prioridade
A Fila de Prioridade (do inglês Priority Queue) é um Tipo Abstrato de Dado (TAD) que opera de forma similar a uma Fila.
Lembramos que o TAD Fila tem comportamento FIFO (first-in first-out), onde o elemento de maior prioridade para sair da fila é o elemento que entrou primeiro na fila.
O conceito de prioridade é explicitado nas Filas de Prioridade através de um valor numérico. Nesse caso, a lógica de prioridade pode operar pelo menor ou pelo maior valor, dependendo da aplicação.
Filas de Prioridade na Computação
Filas de Prioridade são estruturas fundamentais na própria computação. Também são úteis na implementações de algoritmos em grafos, como a busca por árvores geradoras mínimas (aulas futuras).
Por exemplo, quando se envia pacotes de dados a roteadores, existem mecanismos que podem tirar vantagem de valores de prioridade entre pacotes (dados de voz e de download, etc). Uma interpretação cotidiana poderia ser uma fila prioritária por idade, na qual os indivíduos mais velhos seriam sempre atendidos antes dos mais novos.

Operações de uma Fila de Prioridade
Uma Fila de Prioridade é uma estrutura de dados com uma direção pre-definida (vamos assumir maior prioridade para o menor valor), consistindo de 3 operações básicas:
- frente “mais prioritária” (peek min ou find min)
- enfileira (enqueue, push ou insert)
- desenfileira “mais prioritário” (dequeue min, pop min ou extract min)
As operações trabalham com chaves numéricas e, opcionalmente, um conteúdo atrelado a cada chave. Outra operação comum no TAD, embora considerada uma operação interna, é a de redução de chave (decrease key).
Implementações
A implementação do TAD Fila de Prioridade geralmente se dá através de uma implementação de árvores de prioridade denominada heap binário. O heap (ou min heap) é uma árvore binária completa, ou seja, facilmente representada como um vetor, com a seguinte propriedade de heap:
- se x é pai de y, então x≤y


Definição do Conceito Fila de Prioridade em C++
O conceito de fila de prioridade somente requer suas três
operações básicas. Como consideramos uma fila de prioridade
genérica (fila de inteiro, char, etc), definimos um conceito
genérico chamado FilaPrioridadeTAD:
template<typename Agregado, typename Tipo>
concept FilaPrioridadeTAD = requires(Agregado a, Tipo t) {
// requer operação 'frente' mais prioritária
{ a.frente() };
// requer operação 'insere' sobre tipo 't'
{ a.insere(t) };
// requer operação 'remove' mais prioritário
{ a.remove() };
// requer operação 'tamanho'
{ a.tamanho() };
};Note que o tipo genérico pode ser estendido para comportar um elemento interno, além da chave numérica.
Utilização da Fila de Prioridade
Antes de completar as funções, utilizaremos o
FilaPrioridadeTAD:
int main () {
FilaPrioridadeTAD auto h = // ... inicializa tipo
// h.cria();
h.insere(20);
h.insere(10);
h.insere(30);
printf("%c\n", h.frente());
printf("%c\n", h.remove());
h.insere(25);
while(p.tamanho() > 0)
printf("%c\n", h.remove());
// h.libera();
return 0;
}Verifique as impressões em tela: 10 10 20 25 30
Operações em um heap
Implementação heap com vetor
Apesar de sua estrutura de árvore, podemos representá-la eficientemente com um vetor, numa implementação puramente sequencial.


Representação por níveis com N=6 e
MAX_N=7:
| 2 | 3 | 6 | 9 | 4 | 7 | |
0 1 2 3 4 5 6Assim, os dados sempre estarão em um espaço contíguo de memória.
Algoritmo FilaPrioridadeTAD frente
A operação frente retorna o elemento mais prioritário do
heap. Felizmente, ele sempre será a raiz da árvore!


Desafio: verifique se é possível o elemento mais prioritário não estar na raiz do heap.
Algoritmo FilaPrioridadeTAD remove - Parte 1/5
A operação remove em adiciona um novo elemento de acordo
com sua prioridade. Como manter a corretude das propriedades do
heap?
Exemplo: como remover o elemento 2?


Algoritmo FilaPrioridadeTAD remove - Parte 2/5
Para manter a corretude das propriedades do heap, em especial, de uma árvore completa, trocamos o primeiro com o último elemento do vetor.
Exemplo: como remover o elemento 2?


Algoritmo FilaPrioridadeTAD remove - Parte 3/5
Após a troca do último elemento com a raiz, perdemos a propriedade heap.
Como corrigir a árvore? Solução: trocas sucessivas descendo até uma folha.


Mas qual filho trocar? Solução: sempre existe um filho certo, sendo ele o mais prioritário entre os irmãos. Assim trocamos o 7 pelo 3.
Algoritmo FilaPrioridadeTAD remove - Parte 4/5
Ainda assim, seguimos sem a propriedade heap.
Como corrigir a árvore? Solução: trocas sucessivas descendo até uma folha.


Mas qual filho trocar? Solução: sempre existe um filho certo, sendo ele o mais prioritário entre os irmãos. Assim trocamos o 7 pelo 4.
Algoritmo FilaPrioridadeTAD remove - Parte 5/5
Finalmente, recuperamos a propriedade heap.
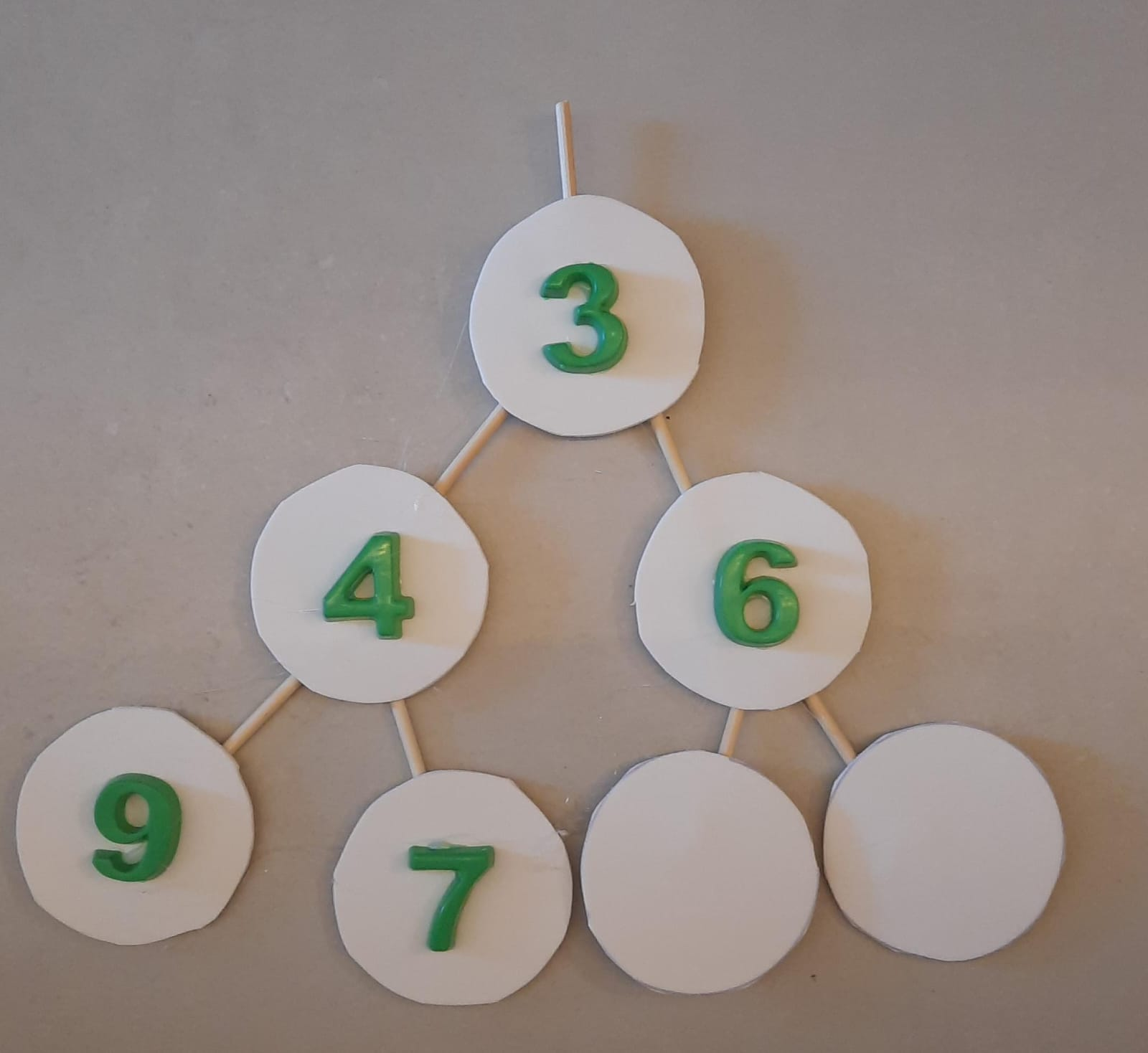

Chegamos na folha, não é preciso mais efetuar trocas.
Algoritmo FilaPrioridadeTAD insere - Parte 1/5
A operação insere em adiciona um novo elemento de acordo
com sua prioridade. Como manter a corretude das propriedades do
heap?
Exemplo: como inserir o elemento 1?
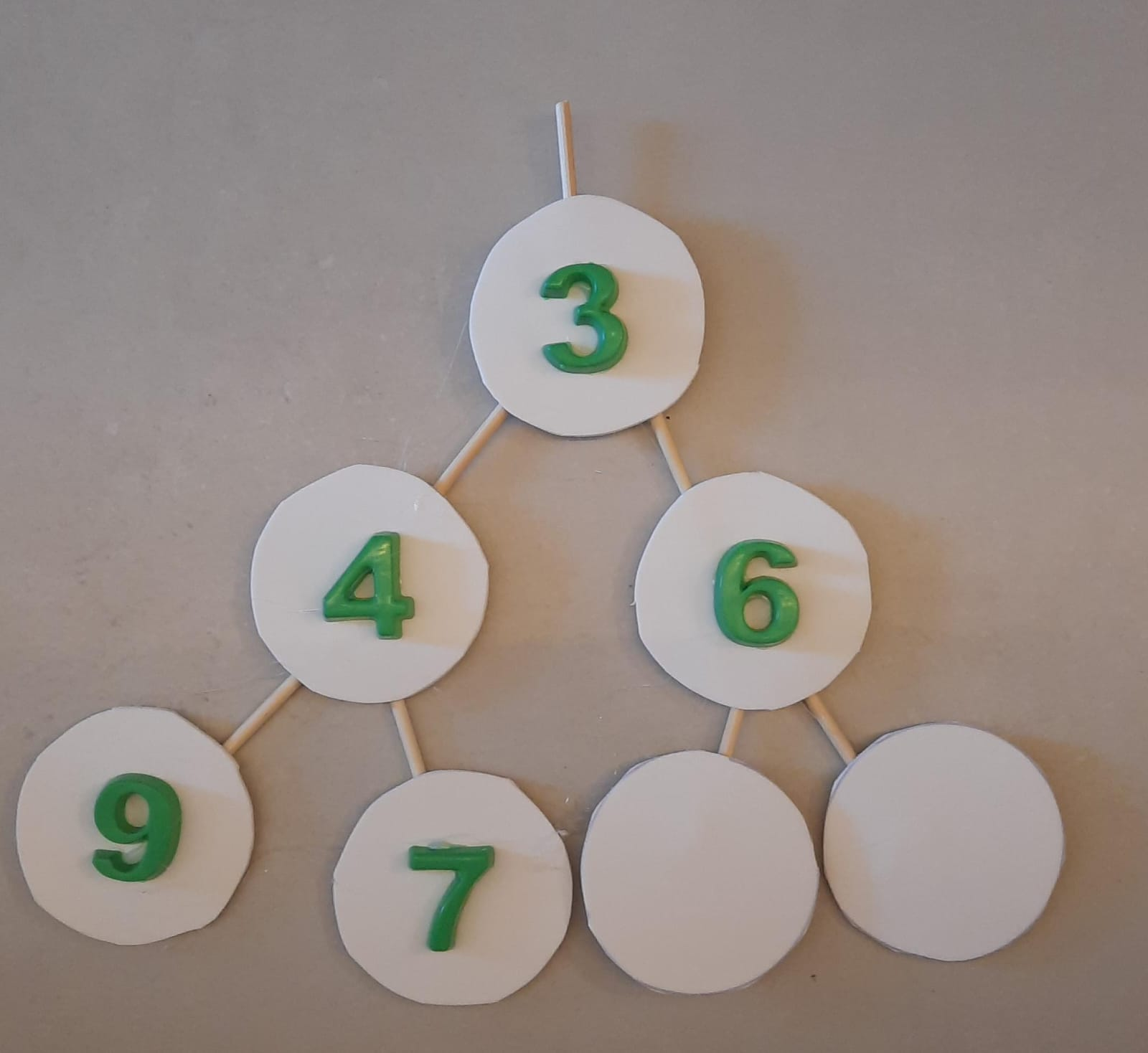

Solução: precisamos manter a árvore completa!
Algoritmo FilaPrioridadeTAD insere - Parte 2/5
Para manter a corretude das propriedades do heap, em especial, de uma árvore completa, adicionamos o elemento na última posição do vetor.
Exemplo: como inserir o elemento 1?


Algoritmo FilaPrioridadeTAD insere - Parte 3/5
Mas agora perdemos a propriedade de heap.
Exemplo: como inserir o elemento 1?
Como corrigir a árvore? Solução: trocas sucessivas subindo até a raiz.

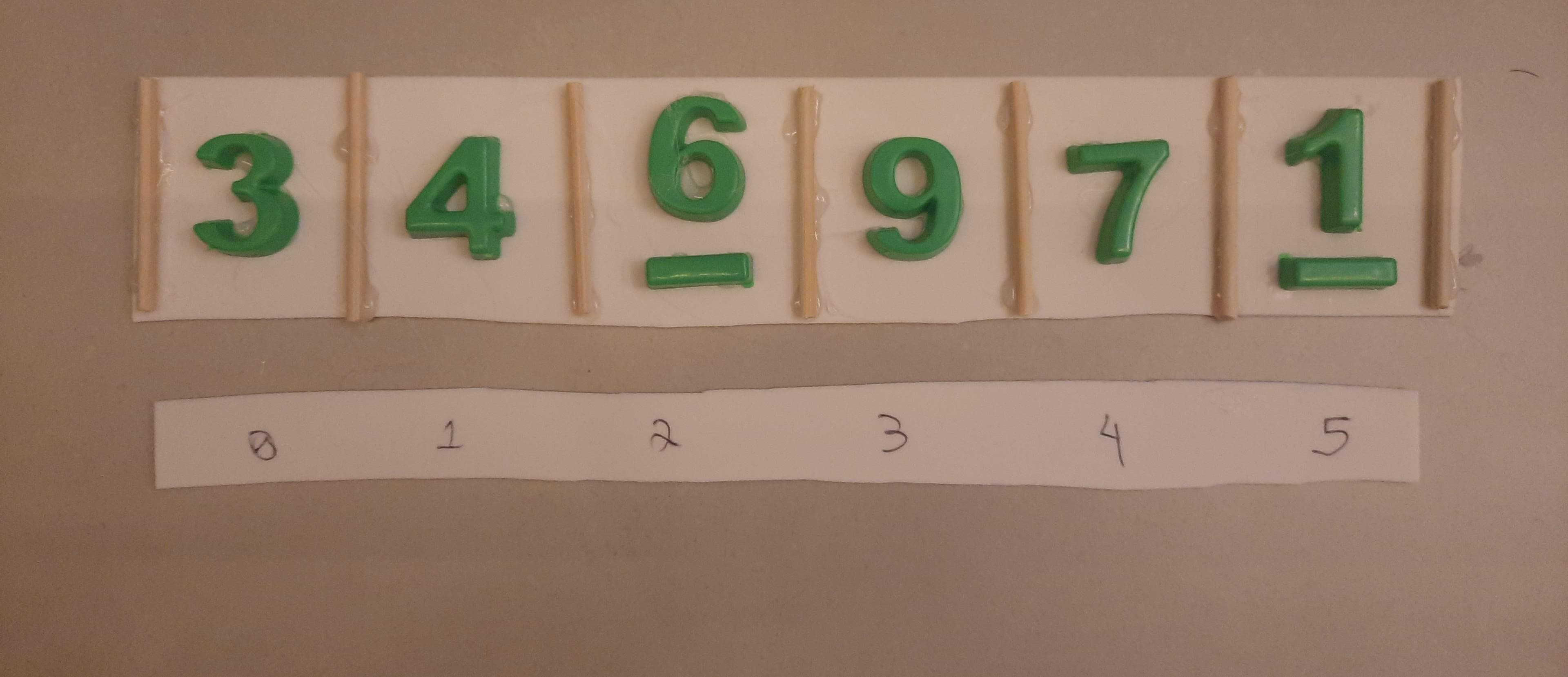
Mas onde está o pai da posição 5 no vetor? Fácil, pai(5)=⌊(5−1)/2⌋=2
Algoritmo FilaPrioridadeTAD insere - Parte 4/5
Mas seguimos sem a propriedade de heap.
Exemplo: como inserir o elemento 1?
Como corrigir a árvore? Solução: trocas sucessivas subindo até a raiz.
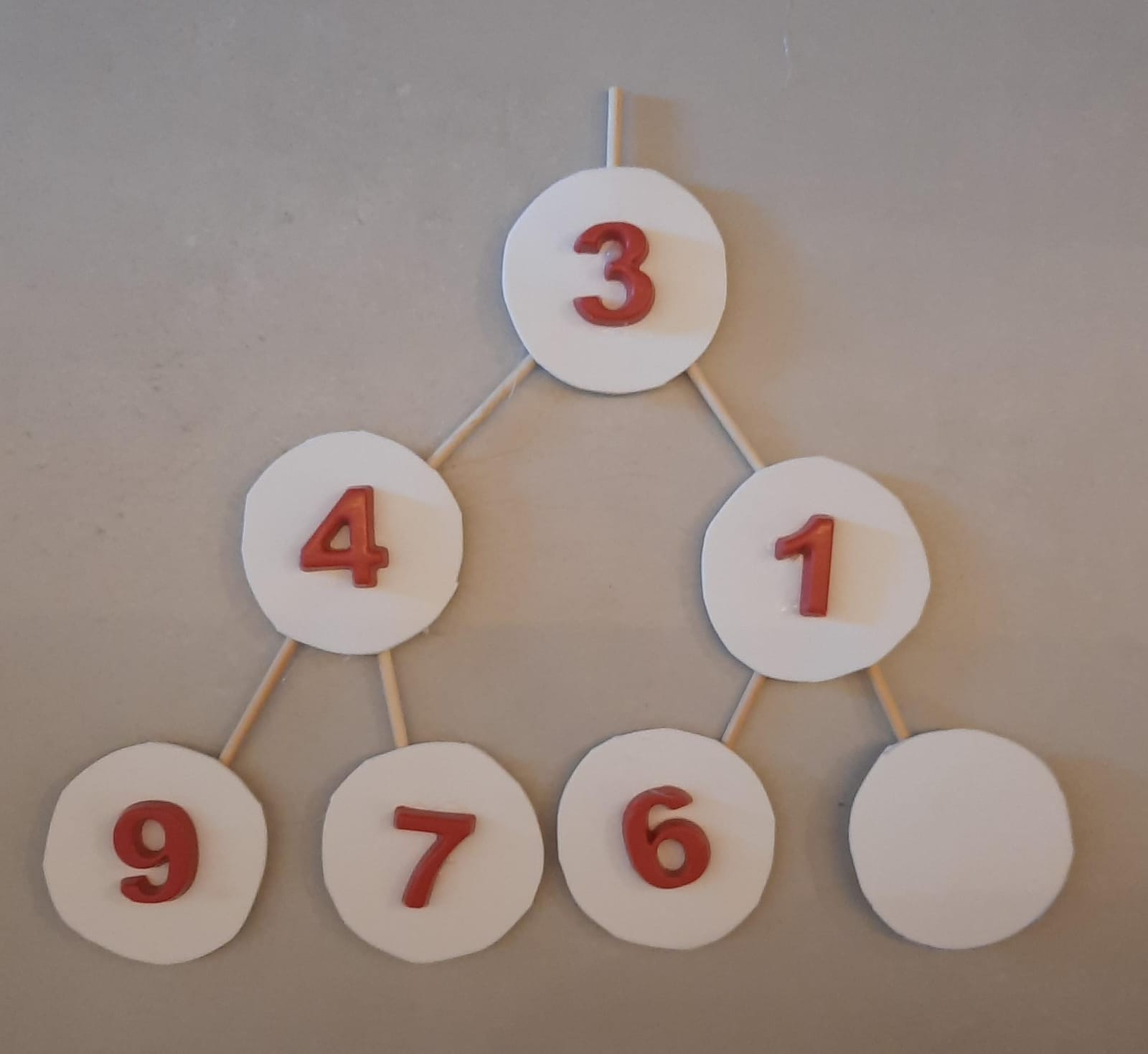

Trocamos então o elemento na posição 2 pelo seu pai.
Algoritmo FilaPrioridadeTAD insere - Parte 5/5
Finalmente, recuperamos a propriedade de heap.
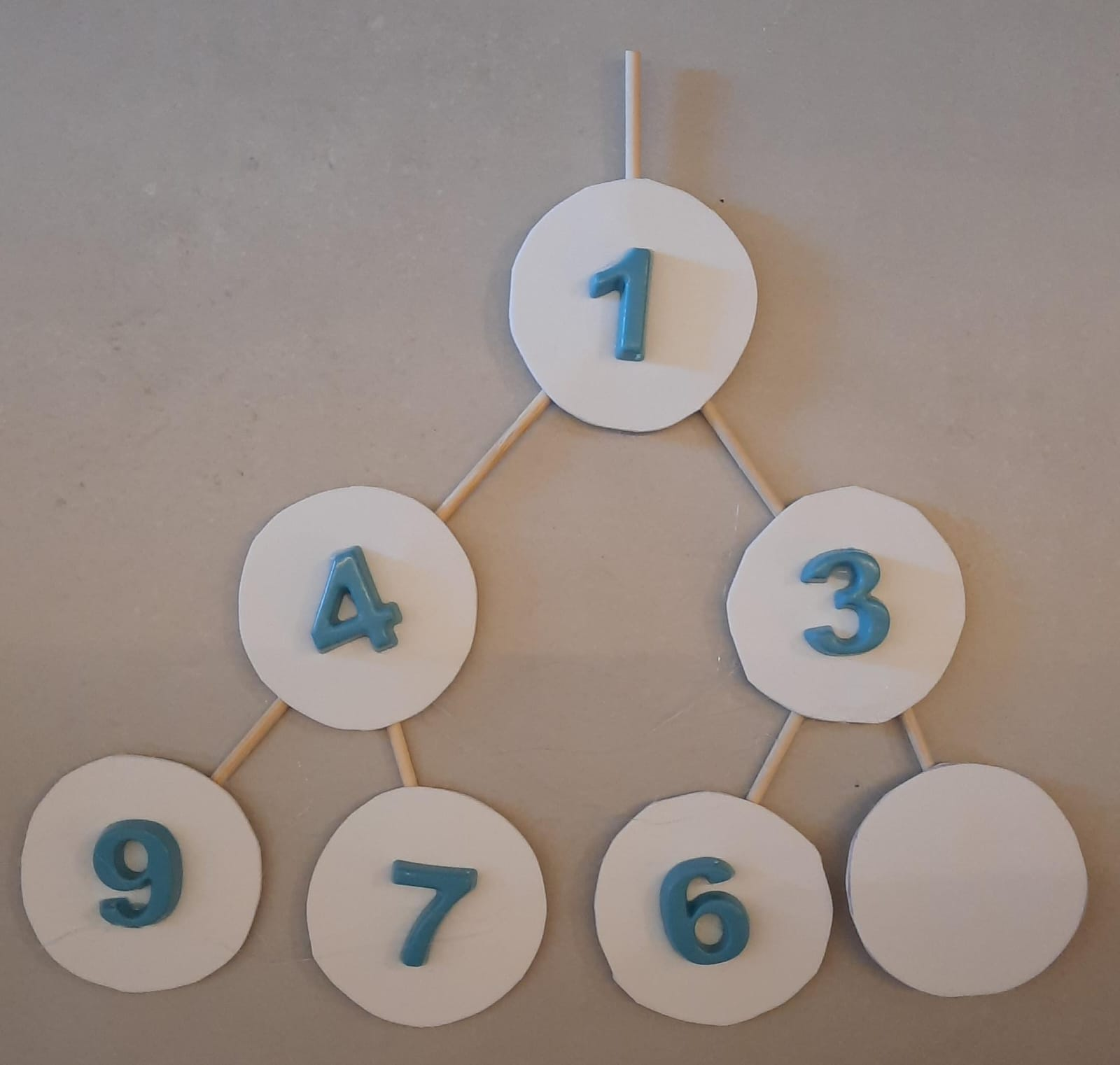
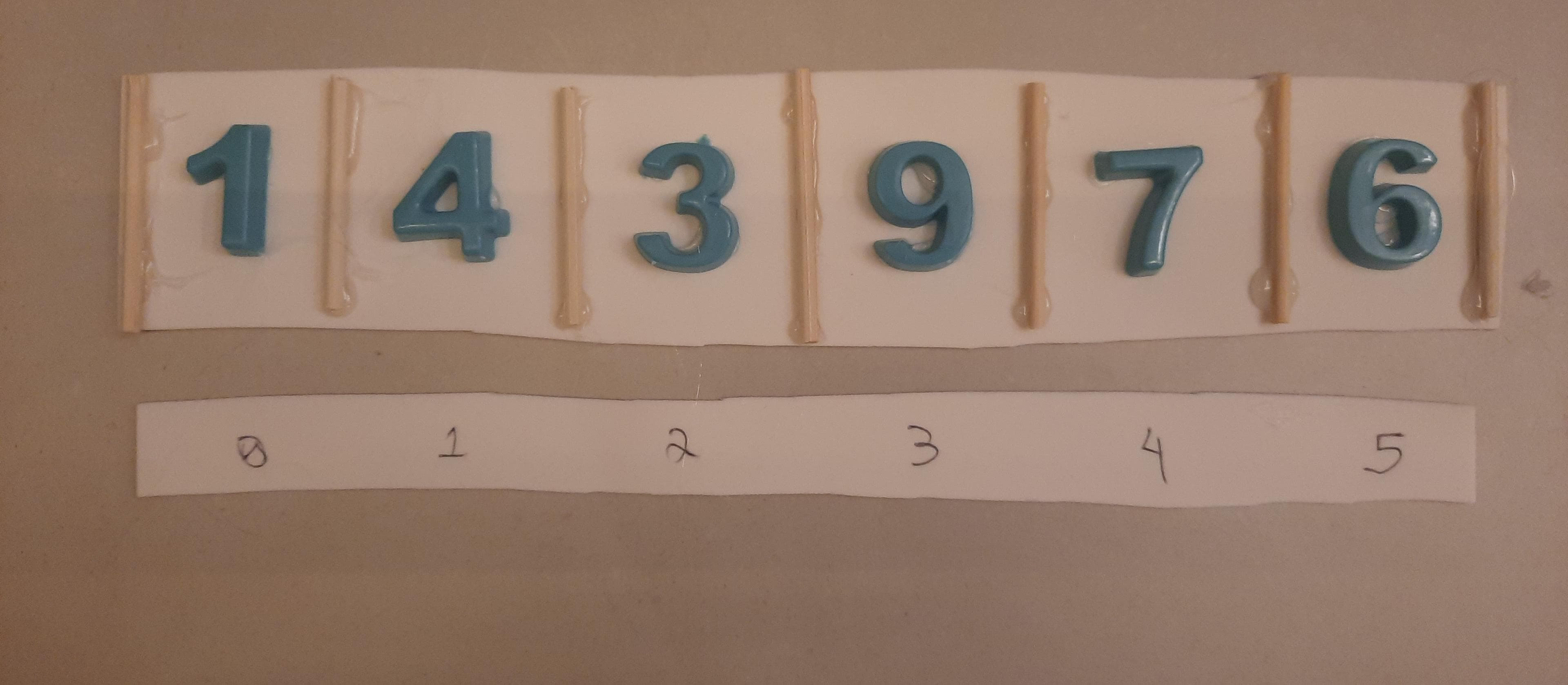
Finalizamos a inserção do elemento 1.
Implementação Heap em C/C++
Aula: Fila de Prioridade - Parte II
Prof. Igor Machado Coelho
https://github.com/igormcoelho/curso-estruturas-de-dados-i
Revisão 18/06/2025
Implementação Heap1
Consideraremos uma fila sequencial com, no máximo, MAX_N
elementos do tipo caractere.
constexpr int MAX_N = 50; // capacidade máxima da fila
struct Heap1 {
int v[MAX_N]; // elementos na fila
int N; // num. de elementos na fila
void cria (); // inicializa agregado
void libera(); // finaliza agregado
int frente();
void insere(int chave);
int remove();
};
// verifica se agregado Heap1 satisfaz FilaPrioridadeTAD
static_assert(FilaPrioridadeTAD<Heap1, int>);Implementação Heap1 - cria/libera
A operação cria inicializa a fila para uso, e a função
libera desaloca os recursos dinâmicos.
Implementação Heap1 - frente
A operação frente retorna a raiz do heap, ou seja, o
primeiro elemento. Este é sempre o mais prioritário.
Representação por níveis (árvore completa):
| 3* | 10 | 7 | 11 | 19 | 35 | 8 | 14 | 12 | 22 | 30 | 44 |Implementação Heap1 - pai e filho
Métodos auxiliares pai e filho.
Implementação Heap1 - sobe
A operação sobe compara sistematicamente um nó com seu
pai, efetuando trocas enquanto a prioridade estiver incorreta. Custo:
proporcional ao nível.
Implementação Heap1 - insere
O método insere coloca o novo elemento no final do heap
e invoca a operação sobe. Custo: altura da árvore.
Implementação Heap1 - desce
A operação desce compara um nó com seus filhos, trocando
enquanto a prioridade for incorreta. Custo: proporcional ao nível.
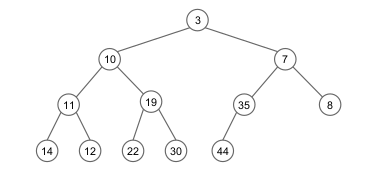
Representação por níveis:
| 3 | 10 | 7 | 11 | 19 | 35 | ...
| 8 | 14 | 12 | 22 | 30 | 44 |Implementação Heap1 - remove
O método remove troca o primeiro com último elemento e
invoca a operação desce. Custo: altura da árvore.
Heapify / Constroi
A construção de um heap através de um vetor é chamada de heapify. É possível efetuar a construção de forma iterativa, através dos métodos sobe ou desce.
Como vimos anteriormente, o método sobe custa, no máximo, o nível do nó, enquanto o método desce custa, no máximo, a altura do nó.
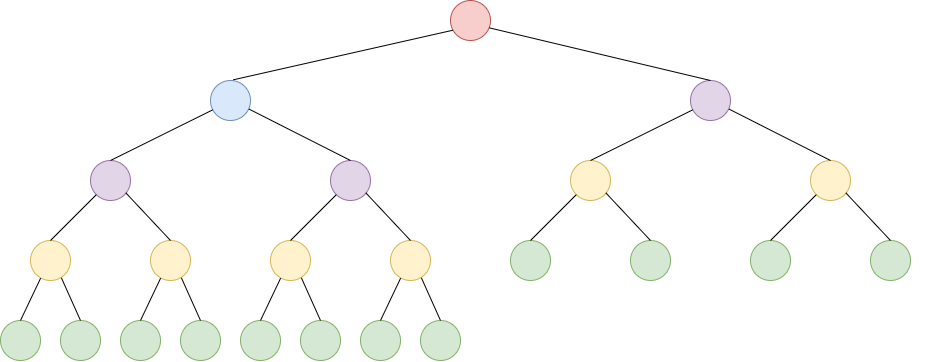
Veja as alturas dos nós (N=23): vermelho(5), azul(4), roxo(3), amarelo(2), verde(1). Metade dos nós (12) tem altura 1.
Heapify com sobe
A construção do heap (N=31) com o método sobe opera sequencialmente a partir dos nós 1,2,3,4..., e a raiz não efetua nenhuma troca. Cada elemento folha (≈N/2) irá incorrer em O(h=⌈lgN⌉) trocas, no pior caso, tendo assim complexidade O(NlgN).
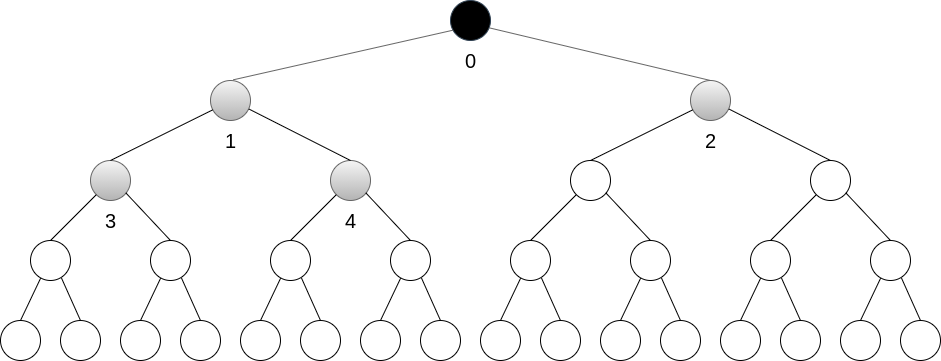
nós: | 0 | 1 | 2 | 3 | 4 | ... ->Método Heapify com sobe
Heapify com desce
A construção do heap (N=31) com o método desce toma vantagem de que as folhas (≈N/2) tem altura 1, portanto não necessitando de troca alguma. O método opera sequencialmente em ordem decrescente a partir do nó ⌊N/2⌋−1=14 como 14,13,12,11,10,.... Note que um único elemento (a raiz) irá incorrer em O(h=⌈lgN⌉) trocas, sendo a complexidade O(NlgN) superestimada neste caso.
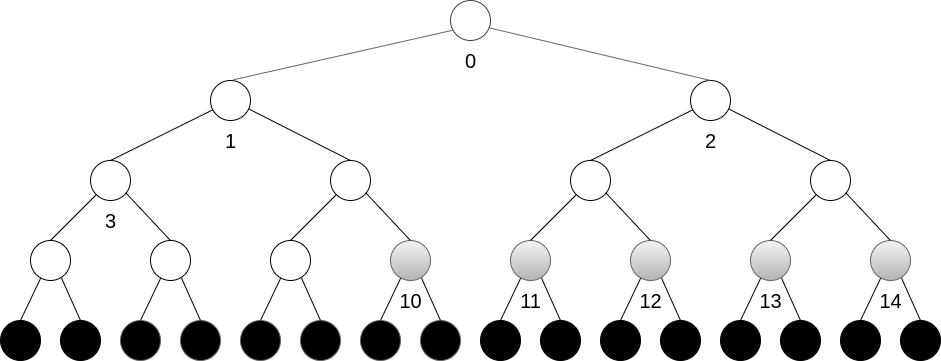
nós: | 0 | 1 | ... <- | 10 | 11 | 12 | 13 | 14 | ...Método Heapify com desce
Análise do Método Heapify com desce
Consideramos uma árvore com N nós e h=⌈lgN⌉ níveis. No nível 1, um único nó (a raiz) efetua h−1 trocas, no pior caso. Por outro lado, existem 2h−1 folhas que não fazem nenhuma troca.
De forma geral, no nível i, cada um dos 2i−1 nós efetuam h−i trocas, no pior caso, totalizando ∑i=1h−1(2i−1(h−i)) trocas.
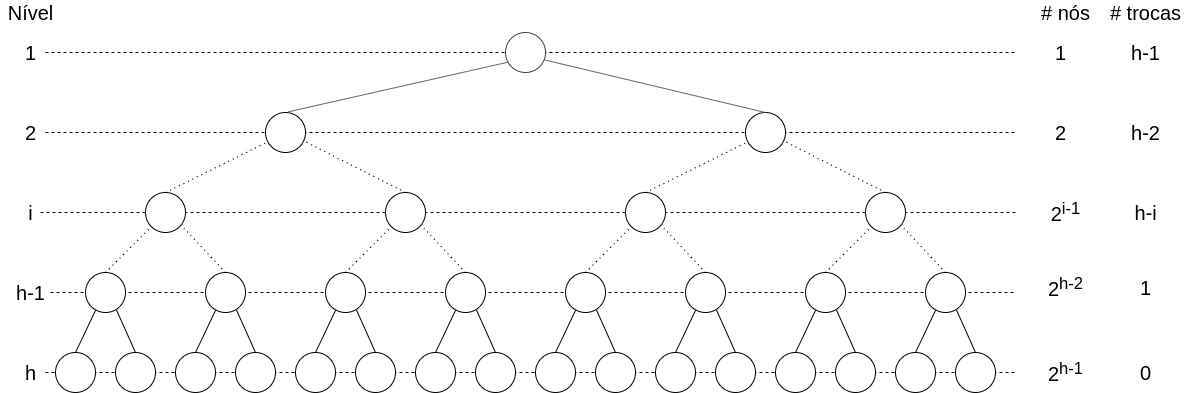
Análise do Método Heapify com desce
Temos que ∑i=1h−1(2i−1(h−i))=2h−(h+1), dado que ∑i=0m2i=2m+1−1. Desmembramos em cada linha i abaixo as h−i ocorrências de 2i−1, de i=1 até h−1. Efetuamos então uma soma por colunas.
i=1:i=2:i=3:i=4:i:i=h−2:i=h−1:++++++=1248⋯2h−32h−2∑i=0h−22i++++++++1248⋯2h−3∑i=0h−32i+⋯++⋯++⋯++⋯++⋯+⋯+1248∑i=032i++++124∑i=022i+++12∑i=012i++1∑i=002iH−1
===(2h−1−1)+(2h−2−1)2h−1+2h−2∑i=0h−12i−h+⋯++⋯+=(23−1)+(22−1)+(21−1)23+22+21−(h−1)2h−(h+1)■
Análise do Método Heapify com desce
Temos então que o total de trocas do heapify é 2h−(h+1), e considerando uma altura h=⌈lgN⌉=O(lgN), temos:
2O(lgN)−(O(lgN)+1)=O(N)
Na prática, para N=31 e, portanto, h=5, temos: 8×1+4×2+2×3+1×4=26 trocas.
Veja código em materiais.
Agradecimentos ao Prof. Fabiano Oliveira, pelo embasamento dessa prova.
Bibliografia Recomendada
Além da bibliografia do curso, recomendamos para esse tópico:
- Szwarcfiter, J.L; Markenzon, L. Estruturas de Dados e seus Algoritmos. Rio de Janeiro, LTC, 1994. Bibliografia Adicional:
- Cerqueira, R.; Celes, W.; Rangel, J.L. Introdução a estruturas de dados: com técnicas de programação em C. Editora, 2004.
- Cormen, T.H.; Leiserson, C.E.; Rivest, R.L.; Stein Algoritmos: Teoria e Prática. Ed. Campus, 2002.
- Cormen, T.H.; Leiserson, C.E.; Rivest, R.L.; Stein, C. Introduction to Algorithms, 3rd ed.. The MIT Press, 2009.
- Preiss, B.R. Estruturas de Dados e Algoritmos Ed. Campus, 2000;
- Knuth, D.E. The Art of Computer Programming - Vols I e III. 2nd Edition. Addison Wesley, 1973.
- Graham, R.L., Knuth, D.E., Patashnik, O. Matemática Concreta. Segunda Edição, Rio de Janeiro, LTC, 1995.
- Livro “The C++ Programming Language” de Bjarne Stroustrup
- Dicas e normas C++: https://github.com/isocpp/CppCoreGuidelines
Agradecimentos
Pessoas
Em especial, agradeço aos colegas que elaboraram bons materiais, como o prof. Fabiano Oliveira (IME-UERJ), e o prof. Jayme Szwarcfiter cujos conceitos formam o cerne desses slides.
Estendo os agradecimentos aos demais colegas que colaboraram com a elaboração do material do curso de Pesquisa Operacional, que abriu caminho para verificação prática dessa tecnologia de slides.
Software
Esse material de curso só é possível graças aos inúmeros projetos de código-aberto que são necessários a ele, incluindo:
- pandoc
- LaTeX
- GNU/Linux
- git
- markdown-preview-enhanced (github)
- visual studio code
- atom
- revealjs
- groomit-mpx (screen drawing tool)
- xournal (screen drawing tool)
- …
Empresas
Agradecimento especial a empresas que suportam projetos livres envolvidos nesse curso:
- github
- gitlab
- microsoft
- …
Reprodução do material
Esses slides foram escritos utilizando pandoc, segundo o tutorial ilectures:
- https://igormcoelho.github.io/ilectures-pandoc/
Exceto expressamente mencionado (com as devidas ressalvas ao material cedido por colegas), a licença será Creative Commons.
Licença: CC-BY 4.0 2020
Igor Machado Coelho