curso-estruturas-de-dados-i

Dicionários e Árvores de Busca

Pré-Requisitos

São requisitos para essa aula:

Agradecimentos especiais ao prof. Fabiano Oliveira e prof. Fábio Protti, cujo conteúdo didático forma a base desses slides

Tipo Abstrato: Dicionário

Dicionários

O Dicionário (do inglês Dictionary) ou Mapa (do inglês Map) é um Tipo Abstrato de Dado (TAD) que visa oferecer operações de chave-valor. Também é conhecido como mapeamento.

Supondo um mapeamento M do tipo caractere para inteiro, por exemplo:

M:
B -> 120
C -> 150
...

Dicionários na computação

Dicionários são estruturas fundamentais na própria computação.

Por exemplo, algumas linguagens de programação (como Python) oferecem suporte nativo a dicionários:

>>> M = dict()
>>> M['A'] = 100
>>> M['A']
100

Assim como arrays, servem para armazenar um conjunto de dados de certo tipo (estrutura homogênea). Uma diferença em relação a vetores, é que permitem indexação da chave de busca por tipos arbitrários.

Operações de um Dicionário

Um Dicionário requer 3 operações básicas:

Definição do Conceito Dicionário em C++

O conceito de dicionário somente requer suas três operações básicas. Como consideramos um dicionário genérico (mapa de inteiro, char, etc), definimos um conceito genérico chamado DicionarioTAD (note que precisamos de dois tipos genéricos, para chave e valor):

template<typename Agregado, typename TChave, typename TValor>
concept 
DicionarioTAD = requires(Agregado d, TChave c, TValor v) {
   // requer operação 'consulta'
   { d.consulta(c) };
   // requer operação 'adiciona'
   { d.adiciona(c, v) };
   // requer operação 'remove'
   { d.remove(c) };
};

Exemplo: Dicionário de char para int

struct DicionarioCI {
   // ... 
   int consulta(char c) {
      // ...
   }
   void adiciona(char c, int v) {
      // ...
   }
   int remove(char c) {
      // ...
   }
};
// verifica estrutura do DicionarioTAD
static_assert(DicionarioTAD<DicionarioCI, char, int>);

Exemplo de Uso com DicionarioCI

Adiciona pares chave-valor ('A', 100) e ('B', 200). Depois faz consultas e remove chave 'B'.

auto main() -> int {
   DicionarioCI d;
   d.cria();                            // inicializa
   d.adiciona('A', 100);
   d.adiciona('B', 200);
   std::println("{}", d.consulta('A')); // 100
   std::println("{}", d.consulta('B')); // 200
   d.remove('B');                       // 200
   // ...
   d.libera();                          // libera estrutura
   
   return 0;
}

Como implementar dicionários de forma eficiente?

Existem duas formas eficientes de implementação de dicionários:

Árvores de Busca

Problema de Busca

Consideramos o Problema da Busca em que, dados:

Responda: $x$ pertence a $S$?

Em caso positivo, encontrar $s_i$ tal que $s_i = x$.

Desafio: Como organizar os dados de forma a facilitar a operação de busca?

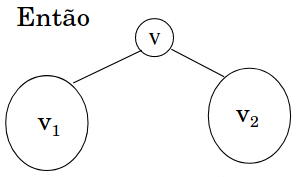
Árvore Binária de Busca: Definição

Podemos utilizar uma Árvore Binária rotulada $T$, tal que:

Relação entre nós numa Árvore Binária de Busca{width=30%}

$T$ é uma Árvore Binária de Busca (ABB)

Árvore Binária de Busca: Exemplo

Exemplos de ABB, contendo nós D, E, F, L, M, N e O.

::::::::::{.columns}

:::::{.column width=45%}

Árvore $A2$ com três folhas{height=40%}

:::::

:::::{.column width=50%}

Árvore $A3$ com cinco folhas{height=40%}

:::::

::::::::::

Estrutura de Árvore Binária

Relembrando (aula de Árvores) a estrutura de árvore binária considerada:

struct NoEnc3 {
   char chave;     // dado armazenado
   NoEnc3* esq;    // filho esquerdo
   NoEnc3* dir;    // filho direito
};

struct ArvoreEnc3 {
  NoEnc3* raiz;    // raiz da árvore
};

Problema da Busca com uma ABB

Podemos resolver o Problema da Busca, com chave de busca $c$, através de uma ABB.

Ideia Geral:

Árvore $A3$ com cinco folhas{height=30%}

Tarefa

Avalie se as árvores abaixo são árvores binárias de busca:

::::::::::{.columns}

:::::{.column width=45%}

Árvore $A1$ com três folhas{height=40%}

:::::

:::::{.column width=50%}

Árvore $A4$ com cinco folhas{height=40%}

:::::

::::::::::

. . .

Solução: nenhuma delas é! Erros: $B < A$ (na A1); $H > K$ (na A4).

Implementação: buscaABB

Implementação da busca em árvores binárias de busca:

std::optional<char> buscaABB(NoEnc3* no, char c) {
   if(!no)
      return std::nullopt;          // chave não encontrada
   if(no->chave == c)
      return std::make_optional(c); // chave encontrada
   if(c < no->chave)
      return buscaABB(no->esq, c);  // recursão esquerda
   else
      return buscaABB(no->dir, c);  // recursão direita
}

Pergunta: Quantos chamadas recursivas esse algoritmo pode precisar?

. . .

Resposta: Em uma árvore degenerada com $N$ nós, até $N$ passos (observe que, nesse caso, $N$ também é a altura da árvore)

Exercício

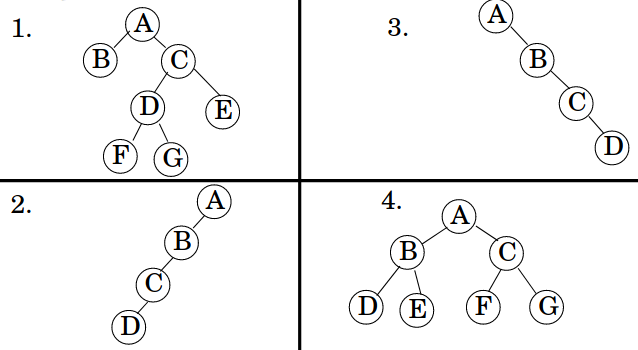
Encontre o pior caso (pior chave de busca) para a execução do algoritmo buscaABB nas quatro árvores abaixo (avalie primeiro se são ou não árvores binárias de busca):

::::::::::{.columns}

:::::{.column width=70%}

{width=90%}

:::::

:::::{.column width=30%}

Árvore $A3$ com cinco folhas{height=40%}

:::::

::::::::::

. . .

Solução: 1. N/A, 2. N/A, 3. E, 4. N/A, Fig.7 L

Árvore Binária de Busca Ótima

Como a buscaABB depende a altura da árvore, qual o melhor caso possível para a busca (menor altura possível) em uma árvore binária com $N$ nós?

Relembrando: uma árvore binária completa (ou cheia/perfeita) possui $\lceil \log_2 (N+1) \rceil$ níveis. Verifique essa afirmação:

::::::::::{.columns}

:::::{.column width=70%}

{width=90%}

:::::

:::::{.column width=30%}

Árvore $A3${height=40%}

:::::

::::::::::

. . .

Solução: 1. N/A, 2. N/A, 3. N/A, 4. $N=7$ e $\log_2 8 = 3$ (Fig.7 tem $\log_2 9 = 4$)

Árvores Balanceadas

Árvores Balanceadas

Um tipo importante de Árvore Binária de Busca é a balanceada, que resolve o problema de degeneração da árvore pelo controle de sua altura.

Tal controle é conseguido pelo cálculo de um fator de balanceamento (FB) para cada nó, definido por: altura do filho esquerdo - altura do filho direito. Observe que se o filho não existe, então sua altura será 0 (zero).

Exercício

Calcule o fator de balanceamento da raiz das quatro árvores abaixo e informe se estão balanceadas:

::::::::::{.columns}

:::::{.column width=70%}

{width=90%}

:::::

:::::{.column width=30%}

Árvore $A3${height=40%}

:::::

::::::::::

. . .

Solução: 1. $1-3=-2$ (não), 2. $0-3=-3$ (não), 3. $3-0=3$ (não), 4. $2-2=0$ (sim), Fig.7 $3-2=1$ (sim)

Implementação de Dicionário com Árvores

Implementação de Dicionário com Árvores

Existem duas implementações populares de árvores balanceadas para dicionários: AVL e rubro-negra.

Iremos explorar a árvore AVL, por sua simplicidade.

Criada em 1962 pelos russos Georgy Adelson-Velsky e Evgenii Landis, ela consegue manter um balanceamento após uma operação de inserção ou remoção.

Basta calcular o fator de balanceamento em cada nó e, caso esteja desbalanceada, algum tipo de operação de rotação será feita.

Nos próximos slides demonstramos as rotações possíveis.

Rotação Simples à Direita

Ocorre quando os fatores de balanceamento são 2 e 1 (ou 0).

Rotacao Simples Vermelha - Z Y X{height=40%}

Após rotação à direita, a árvore fica enraizada em Y, com X à esquerda e Y à direita.

Rotação Simples à Esquerda

Ocorre quando os fatores de balanceamento são -2 e -1 (ou 0).

Rotacao Simples Azul - P Q R{height=40%}

Após rotação à direita, a árvore fica enraizada em Q, com P à esquerda e R à direita.

Rotação Dupla à Direita

Ocorre quando os fatores de balanceamento são 2 e -1. Isso exige duas rotações, uma à esquerda e outra à direita.

::::::::::{.columns}

:::::{.column width=50%}

Rotacao Simples Esquerda do filho X - Z X Y{height=40%}

:::::

:::::{.column width=50%}

Rotacao Simples Direita da raiz Z - Z Y X{height=40%}

:::::

::::::::::

Após rotação à esquerda em X, a árvore fica enraizada em Z, mas ainda desbalanceada como 2 1. Uma nova rotação à direita da raiz Z resolve o problema.

Rotação Dupla à Esquerda

Ocorre quando os fatores de balanceamento são -2 e 1. Isso exige duas rotações, uma à direita e outra à esquerda.

::::::::::{.columns}

:::::{.column width=50%}

Rotacao Simples Direita do filho R - P R Q{height=40%}

:::::

:::::{.column width=50%}

Rotacao Simples Esquerda da raiz P - P Q R{height=40%}

:::::

::::::::::

Após rotação à direita em R, a árvore fica enraizada em P, mas ainda desbalanceada como -2 -1. Uma nova rotação à esquerda da raiz P resolve o problema.

Praticando as Rotações

Considere uma árvore A3 com nós M, D, O, B, F, N, S, E, L. A exclusão de S não acarreta em desbalanceamento. A exclusão de B gera um desbalanceamento no nó D, com fator 0-2=-2 seguido de 0.

Isso indica uma Rotação Simples à Esquerda, no nó D.

::::::::::{.columns}

:::::{.column width=70%}

Árvore $A3${height=30%}

:::::

:::::{.column width=30%}

Árvore $A2${height=30%}

:::::

::::::::::

Qual o final após a rotação? F substitui D, tornando E seu filho à esquerda, seguido de D à esquerda, sendo que o filho à direita de F se torna L. A árvore se torna balanceada.

Bibliografia Recomendada

Além da bibliografia do curso, recomendamos para esse tópico:

Agradecimentos

Pessoas

Em especial, agradeço aos colegas que elaboraram bons materiais, como o prof. Fabiano Oliveira (IME-UERJ), e o prof. Jayme Szwarcfiter cujos conceitos formam o cerne desses slides.

Estendo os agradecimentos aos demais colegas que colaboraram com a elaboração do material do curso de Pesquisa Operacional, que abriu caminho para verificação prática dessa tecnologia de slides.

Software

Esse material de curso só é possível graças aos inúmeros projetos de código-aberto que são necessários a ele, incluindo:

Empresas

Agradecimento especial a empresas que suportam projetos livres envolvidos nesse curso:

Reprodução do material

Esses slides foram escritos utilizando pandoc, segundo o tutorial ilectures:

Exceto expressamente mencionado (com as devidas ressalvas ao material cedido por colegas), a licença será Creative Commons.

Licença: CC-BY 4.0 2020

Igor Machado Coelho

This Slide Is Intentionally Blank (for goomit-mpx)

This site is open source. Improve this page.