curso-estruturas-de-dados-i
Árvores
Pré-Requisitos
São requisitos para essa aula:
- Introdução/Fundamentos de Programação (em alguma linguagem de programação)
- Interesse em aprender C/C++
- Noções de recursividade
- Noções de tipos de dados
- Noções de listas e encadeamento
Agradecimentos especiais ao prof. Fabiano Oliveira e prof. Fábio Protti, cujos conteúdos didáticos formam a base desses slides
Tipo Abstrato: Árvore
Árvore
A Árvore (do inglês Tree) é um Tipo Abstrato de Dado (TAD) que pode assumir duas formas:
- árvore $T$ vazia, denotada por $T = \emptyset$
- árvore $T$ composta por:
- um nó $R$ chamado de nó raiz
- $0$ ou mais árvores disjuntas $T_1$, $T_2$, …, associadas a $R$; tais árvores são chamadas de subárvores
{width=55%}
Nomenclatura
Um conjunto de árvores é chamado floresta
Se T é uma árvore com raiz R, então:
- os nós de T são todas as raízes de subárvores de R, além da raiz de T
- um nó com 0 filhos é chamado de folha (do inglês leaf)
- se um nó F é um filho de um nó P, denominamos P como pai de F
- a raiz é um nó ancestral de todos nós da árvore
- todos os nós da árvore são descendentes do nó raiz
Caminhos
Um caminho em uma árvore é uma sequência de nós com relação filho de ou pai de:
{width=55%}
Exemplos:
- E,C,A
- D,G,I
- C,A,D,G
Tamanho de Caminhos e Níveis
O tamanho de um caminho consiste no número de nós. O nível de um nó é o tamanho de seu caminho até a raiz:
{width=55%}
Nível de: A=1; C=2; F=3; H=4.
Desafio: em cursos de Teoria dos Grafos é provado que existe um único caminho conectando dois nós na árvore. Utilize sua intuição para verificar esta afirmação!
Alturas
A altura de nó X é o tamanho do maior caminho que conecta X a uma folha descendente. Denotamos a altura de $X$ por $h(X)$:
{width=55%}
Alturas: $h(B)=1$; $h(C)=2$; $h(D)=3$; $h(A)=4$.
A altura da árvore é a altura de sua raiz!
No exemplo, $h(T) = h(A) = 4$.
Aridade
Uma árvore é dita ordenada se há uma ordem associada aos filhos de cada nó.
Uma árvore é dita $m$-ária se cada nó é limitado a um máximo de $m$ filhos.
{width=55%}
A árvore acima é ternária (podendo também ser $4$-ária, $5$-ária, $6$-ária, …), mas não é binária!
Filho esquerdo e direito
Em árvores binárias ordenadas de raiz R, a primeira subárvore de cada nó é denominada subárvore à esquerda de R (cuja raiz se chama filho esquerdo), e a segunda é a subárvore à direita de R (cuja raiz se chama filho direito).
{width=50%}
Exemplo: B é filho esquerdo e C é filho direito de A
Estritamente $m$-ária
Uma árvore estritamente $m$-ária é aquela na qual cada nó possui exatamente $0$ ou $m$ filhos.
{width=50%}
Exemplo: Considere a inclusão de um filho à esquerda de C.
Observação: Chamada pelo NIST de full binary tree, embora também seja preferivelmente chamada de própria (ou proper).
Árvore Cheia ou Perfeita
Uma árvore $m$-ária cheia (ou perfeita) é aquela na qual todo nó com alguma subárvore vazia está no último nível.
{width=40%}
Observação: Chamada pelo NIST de perfect binary tree (ou perfect k-ary tree), embora também seja chamada de full ou, preferencialmente perfect.
Árvore Completa
Uma árvore $m$-ária completa é aquela na qual todo nó com alguma subárvore vazia está no último ou penúltimo níveis, estando os nós do último nível completamente preenchidos da esquerda para a direita.
{width=40%}
Observação: Chamada pelo NIST de complete binary tree. Note que alguns autores consideram essa mesma definição para árvores cheias ou perfeitas. O ponto fundamental é a facilidade de implementação em vetores (vide próximos slides). [Knuth97]1
Desafios
-
Qual a altura máxima de uma árvore binária com $n$ nós?
-
Qual a altura máxima de uma árvore estritamente binária com n nós?
-
Qual a altura mínima de uma árvore binária com n nós?
-
Numa árvore binária cheia com n nós, qual o número de nós no último nível?
. . .
Solução: $n$, $(n+1)/2$, $\lceil lg(n+1)\rceil$, $(n+1)/2$
Implementações
Implementações de Árvores
Apresentaremos dois tipos de implementação para o TAD Árvore: Sequencial e Encadeada.
Note que, nesse momento, não apresentaremos operações sobre o TAD Árvore, focando somente em sua representação interna. A razão é que existem diversos tipos específicos de árvores, que apresentam operações distintas no TAD, de acordo com seu propósito.
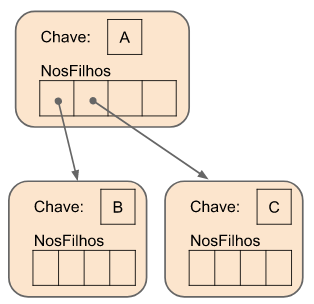
Implementação Encadeada 1 ($m$-ária)
Consideramos uma implementação de árvore $m$-ária, com alocação encadeada de nós (alocação interna sequencial para filhos).
constexpr int M = 3; // aridade M=3 (ternária)
class NoEnc1
{
public:
char chave // dado armazenado
NoEnc1* nosFilhos[M]; // ponteiros para filhos
};
class ArvoreEnc1
{
public:
NoEnc1* raiz; // raiz da árvore
};
Implementação Encadeada 1 ($m$-ária)
{width=40%}
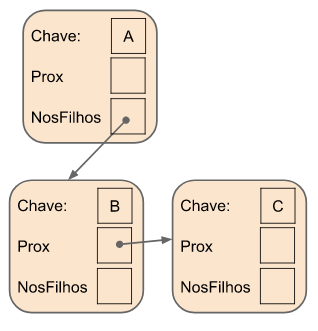
Implementação Encadeada 2 ($m$-ária)
Consideramos uma implementação de árvore $m$-ária, com alocação encadeada de nós.
constexpr int M = 3; // aridade M=3 (ternária)
class NoEnc2
{
public:
char chave; // dado armazenado
NoEnc2* prox; // proximo elemento
NoEnc2* nosFilhos; // ponteiro único para filhos
};
class ArvoreEnc2
{
public:
NoEnc2* raiz; // raiz da árvore
};
Implementação Encadeada 2 ($m$-ária)
Consideramos uma implementação de árvore $m$-ária, com alocação encadeada de nós.
{width=40%}
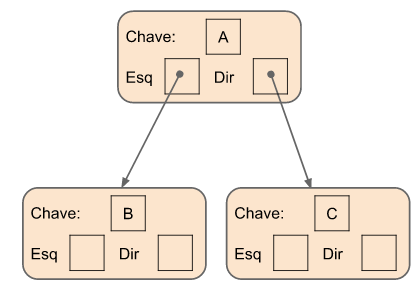
Implementação Encadeada 3 (binária)
Note que podemos reescrever os ponteiros de NoEnc2 com os termos esq e dir (nó esquerdo e nó direito).
class NoEnc3
{
public:
char chave; // dado armazenado
NoEnc3* esq; // filho esquerdo
NoEnc3* dir; // filho direito
};
class ArvoreEnc3
{
public:
NoEnc3* raiz; // raiz da árvore
};
Implementação Encadeada 3 (binária)
Consideramos uma implementação de árvore binária, com alocação encadeada de nós.
{width=40%}
Implementação Encadeada 4 (binária) - unique_ptr
Note que podemos reescrever os ponteiros de NoEnc3 utilizando unique_ptr, para maior segurança:
class NoEnc4
{
public:
char chave; // dado armazenado
std::unique_ptr<NoEnc4> esq; // filho esquerdo
std::unique_ptr<NoEnc4> dir; // filho direito
};
class ArvoreEnc4
{
public:
std::unique_ptr<NoEnc4> raiz; // raiz da árvore
};
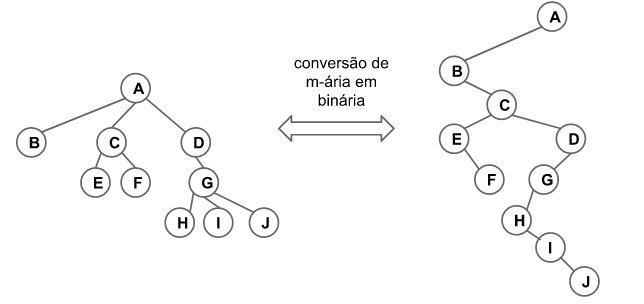
Conversão para Árvores Binárias
Observamos pelas implementações NoEnc2 e NoEnc3 que uma árvore $m$-ária qualquer pode ser convertida para uma árvore binária. Isso reforça a importância do estudo de implementações eficientes para árvores binárias.
{width=70%}
Implementação Sequencial
As Árvores com Implementação Sequencial utilizam um array para armazenar os dados. Assim, os dados sempre estarão em um espaço contíguo de memória.
Desafio: quanto espaço é necessário para armazenar uma árvore qualquer com altura $h$?
Implementação ArvoreSeq1
Consideraremos uma árvore sequencial com, no máximo, MAX_N elementos do tipo caractere.
constexpr int MAX_N = 50; // capacidade máxima da árvore
class ArvoreSeq1
{
public:
char elem [MAX_N]; // elementos na fila
};
Desafio: Quantos níveis cabem nessa árvore? $\lceil log_2(50+1) \rceil = 6$
Desafios na ArvoreSeq1
Note que, para esse fim, somente as árvores completas terão maior eficiência, utilizando uma representação por níveis.
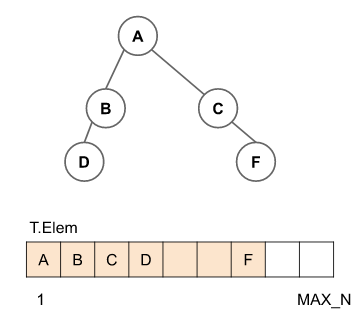{width=40%}
Desafio: onde fica o primeiro elemento de cada nível da árvore $T$?
Localização na ArvoreSeq1
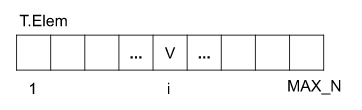
Dado um nó $V$ na posição $i$ da árvore sequencial $T$, em que posição estão:
- o pai de $V$?
- os filhos de $V$?
{width=50%}
. . .
Resposta: considerando contagem 1..MAX_N, estarão respectivamente nas posições $\lfloor i/2 \rfloor$ (pai), $2i$ e $2i+1$ (filhos).
Desafio: considere a contagem 0..MAX_N-1 e refaça o cálculo.
. . .
Solução: posições $\lfloor (i-1)/2 \rfloor$ (pai), $2i+1$ e $2i+2$ (filhos).
Fim implementações
Fim parte de implementações.
Operações em Árvores
Percursos em Árvores
Como “imprimir” uma árvore?
Estruturas lineares tem uma intuição mais direta para o conceito de impressão, mas para estruturas arbóreas isso já não é tão direto. Além da impressão, muitas vezes é desejável efetuar outras operações ou visitas em nós de uma árvore.
Operações de Percursos em Árvore (do inglês, tree traversals) apresentam uma solução para isso:
- Percurso de pré-ordem (do inglês, preorder)
- Percurso de pós-ordem (do inglês, postorder)
- Percurso em-ordem ou ordem simétrica (do inglês, inorder)
Percursos: definições e aplicações
No percurso de pré-ordem, o nó é visitado primeiro, depois os filhos esquerdos, e finalmente, são visitados os filhos direitos.
- Aplicação: impressão da ordem de visita (pilha de execução) para algoritmos recursivos em árvore.
No percurso de pós-ordem, os filhos esquerdos são visitados primeiro, depois os filhos direitos, e finalmente o nó é visitado.
- Aplicação: calcular altura de um nó (note que a altura de um nó depende da altura de seus filhos).
No percurso em-ordem, os filhos esquerdos são visitados primeiro, depois o nó é visitado, e finalmente os filhos direitos são visitados.
- Aplicação: impressão “visual” da árvore como caracteres na tela (desafio!). Visita ordenada em árvores com propriedades de busca e mapas (próxima aula).
Percurso Pré-ordem
void preordem(auto* no) {
if(no) {
printf("%c\n", no->chave); // operação ou "visita"
preordem(no->esq);
preordem(no->dir);
}
}
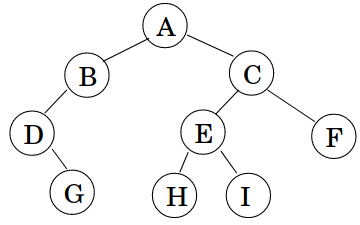{width=50%}
Pratique: Pré-ordem
Apresente o percurso de pré-ordem para as árvores abaixo:
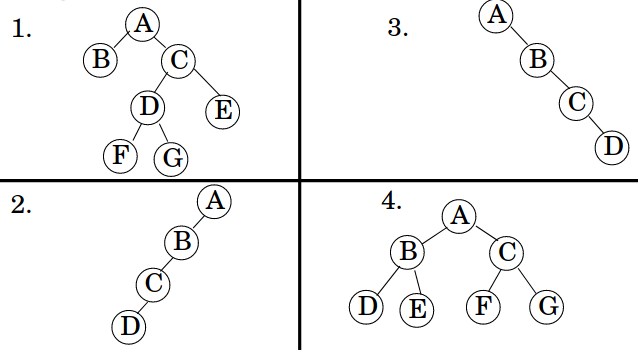{width=70%}
. . .
Solução: 1. ABCDFGE 2. ABCD 3. ABCD 4. ABDECFG
Percurso Pós-ordem
void posordem(auto* no) {
if(no) {
posordem(no->esq);
posordem(no->dir);
printf("%c\n", no->chave); // operação ou "visita"
}
}
{width=50%}
Pratique: Pós-ordem
Apresente o percurso de pós-ordem para as árvores abaixo:
{width=70%}
. . .
Solução: 1. BFGDECA 2. DCBA 3. DCBA 4.DEBFGCA
Percurso Em-ordem (ordem simétrica)
void emordem(auto* no) {
if(no) {
emordem(no->esq);
printf("%c\n", no->chave); // operação ou "visita"
emordem(no->dir);
}
}
{width=50%}
Pratique: Em-ordem
Apresente o percurso de ordem simétrica para as árvores abaixo:
{width=70%}
. . .
Solução: 1. BAFDGCE 2. DCBA 3. ABCD 4. DBEAFCG
Fim percursos
Fim parte de percursos.
Bibliografia Recomendada
Além da bibliografia do curso, recomendamos para esse tópico:
- Szwarcfiter, J.L; Markenzon, L. Estruturas de Dados e seus Algoritmos. Rio de Janeiro, LTC, 1994. Bibliografia Adicional:
- Cerqueira, R.; Celes, W.; Rangel, J.L. Introdução a estruturas de dados: com técnicas de programação em C. Editora, 2004.
- Cormen, T.H.; Leiserson, C.E.; Rivest, R.L.; Stein Algoritmos: Teoria e Prática. Ed. Campus, 2002.
- Cormen, T.H.; Leiserson, C.E.; Rivest, R.L.; Stein, C. Introduction to Algorithms, 3rd ed.. The MIT Press, 2009.
- Preiss, B.R. Estruturas de Dados e Algoritmos Ed. Campus, 2000;
- Knuth, D.E. The Art of Computer Programming - Vols I e III. 2nd Edition. Addison Wesley, 1973.
- Graham, R.L., Knuth, D.E., Patashnik, O. Matemática Concreta. Segunda Edição, Rio de Janeiro, LTC, 1995.
- Livro “The C++ Programming Language” de Bjarne Stroustrup
- Dicas e normas C++: https://github.com/isocpp/CppCoreGuidelines
Agradecimentos
Pessoas
Em especial, agradeço aos colegas que elaboraram bons materiais, como o prof. Fabiano Oliveira (IME-UERJ), e o prof. Jayme Szwarcfiter cujos conceitos formam o cerne desses slides.
Estendo os agradecimentos aos demais colegas que colaboraram com a elaboração do material do curso de Pesquisa Operacional, que abriu caminho para verificação prática dessa tecnologia de slides.
Software
Esse material de curso só é possível graças aos inúmeros projetos de código-aberto que são necessários a ele, incluindo:
- pandoc
- LaTeX
- GNU/Linux
- git
- markdown-preview-enhanced (github)
- visual studio code
- atom
- revealjs
- groomit-mpx (screen drawing tool)
- xournal (screen drawing tool)
- …
Empresas
Agradecimento especial a empresas que suportam projetos livres envolvidos nesse curso:
- github
- gitlab
- microsoft
- …
Reprodução do material
Esses slides foram escritos utilizando pandoc, segundo o tutorial ilectures:
- https://igormcoelho.github.io/ilectures-pandoc/
Exceto expressamente mencionado (com as devidas ressalvas ao material cedido por colegas), a licença será Creative Commons.
Licença: CC-BY 4.0 2020
Igor Machado Coelho
This Slide Is Intentionally Blank (for goomit-mpx)
-
[Knuth97] Donald E. Knuth, The Art of Computer Programming, Addison-Wesley, volumes 1 and 2, 2nd edition, 1997. ↩